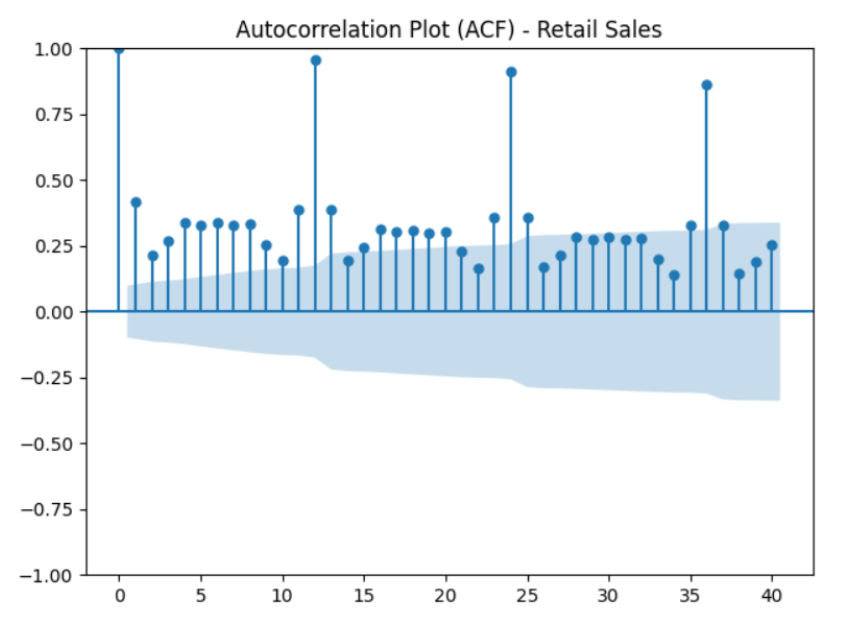
An Autocorrelation function plot shows how each observation in a time series is correlated with its past values at different lags (Forecasting using Lags).
In a Stationary Time Series, autocorrelations typically decay quickly toward zero as the lag increases. This indicates that past values have decreasing influence on future values over time.
In this case, however, we observe that autocorrelations remain high across multiple lags. This suggests:
- The presence of a trend, since values are persistently related over time (Trends in Time Series).
- The presence of seasonality, if there are repeating peaks at specific lag intervals (Seasonality in Time Series).
Interpretation: The slow decay and repeated high correlations confirm that the series is non-stationary. When examining the ACF plot, you are primarily looking for:
- Decay pattern: Rapid decay indicates stationarity; slow decay suggests non-stationarity.
- Significant peaks: Regular spikes at certain lags indicate seasonality.
- Correlation magnitude: High correlations at large lags indicate a trend or long-term dependencies.
