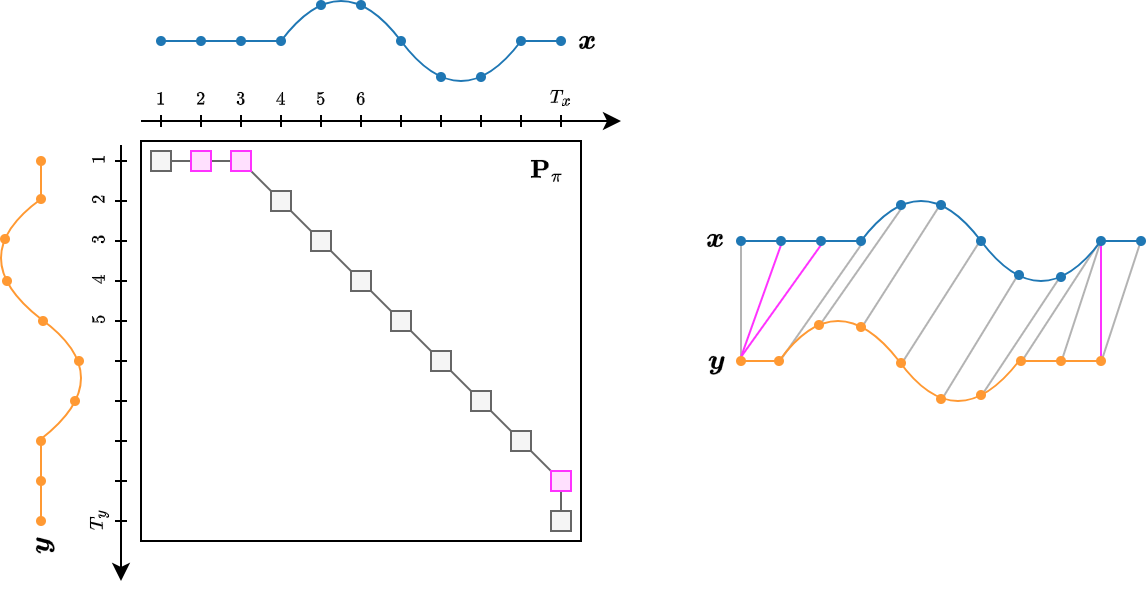
Dynamic Time Warping

Dynamic Time Warping (DTW) is a method for measuring similarity between time series that may vary in speed, phase, or length. DTW seeks for the temporal alignment (a matching between time indexes of the two time series) that minimizes Euclidean distance between the aligned series.

There are different variations and extensions.

Conceptual Overview

Dynamic Time Warping computes an optimal alignment between two time series by stretching or compressing segments along the time axis to minimize overall distance.

Unlike Euclidean distance (which assumes perfect time alignment), DTW allows local warping — making it robust to temporal distortions such as shifts, delays, or different speeds of progression.

Formally, for two sequences $X=(x_1,\dots ,x_n)$ and $Y=(y_1,\dots ,y_m)$, DTW finds a warping path $W=(w_1,\dots ,w_k)$ minimizing

$$DTW(X,Y)=\underset{W}{\min }\sum _{(i,j)\in W}d(x_i,y_j)$$

subject to continuity, monotonicity, and boundary conditions.

DTW will change if curves are stretched or squeezes. It is invariant to translation.

Euclidean distance is not suitable for this.

Common Use Cases

Clustering Time Series

• DTW is often used as a distance metric in clustering algorithms such as $k$-means (with DTW distance) or hierarchical clustering.
• It groups together time series with similar shape or evolution pattern, even if they are temporally misaligned.

Time Series Classification

• Used with $k$-Nearest Neighbours (k-NN) classifiers:
• Each new sequence is classified by finding the training series with the smallest DTW distance.
• Especially common when you have small datasets or irregular time axes.

Anomaly Detection

• DTW can detect deviations from normal temporal patterns.
• Comparing a new sequence against a reference template: a high DTW distance indicates an anomaly.

Pattern Matching / Template Matching

• DTW is used to locate subsequences that match a reference pattern within a larger time series.
• The technique can handle stretching or compression of the pattern.

Forecast Evaluation / Model Comparison

• Used to assess the shape similarity between predicted and observed series.
• More robust than RMSE or MAE when there are temporal shifts between predicted and actual peaks.

When to Use DTW

Condition	DTW Appropriate?
Series differ in time length	✅
Series have similar shapes but different timing	✅
Series are strictly aligned (same timestamps)	❌ (correlation is simpler)
Very large datasets (millions of series)	⚠️ Computationally expensive

Clustering

• Cluster using Dendrograms (find number of clusters) or KNN
• Use Time Series Cluster Kernel TCK
• Use Dimensionality Reduction to visualise.

Related:

• Correlated Time Series