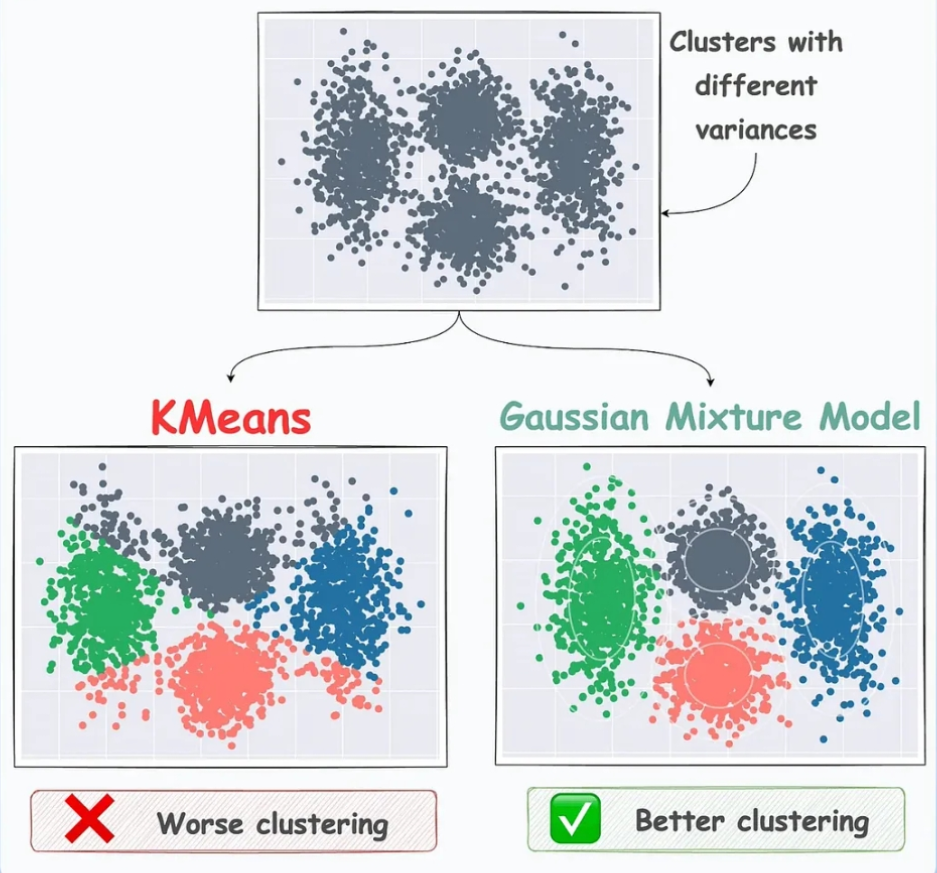
Gaussian Mixture Models

Gaussian Mixture Models (GMMs) represent data as a mixture of multiple Gaussian distributions, with each cluster corresponding to a different Gaussian component. GMMs are more effective than K-means because they consider the distributions of the data rather than relying solely on distance metrics.

Soft Clustering technique.

In ML_Tools see: gaussian_mixture_model_implementation.py

Kmeans vs GMM

GMMs can have difference Covariance Structures

Key Concepts

• Gaussian Components: Each Gaussian distribution is characterized by its mean and Covariance.
• Likelihood: The likelihood of a data point belonging to a cluster is given by the formula: $$P(X|C_k)={\pi }_k\cdot \mathcal{N}(X|{\mu }_k,{\Sigma }_k)$$ where $P(X|C_k)$ is the probability of data point $X$ given cluster $C_k$, ${\pi }_k$ is the prior probability of cluster $C_k$, and $\mathcal{N}$ is the Gaussian distribution.
• Expectation-Maximization (EM) Algorithm: GMMs utilize the EM algorithm to iteratively optimize the parameters of the Gaussian components.

Advantages of GMMs

• Complex Data Distributions: GMMs can capture complex data distributions, unlike K-means, which only considers distance metrics.
• Probabilistic Framework: GMMs provide a probabilistic framework for clustering, allowing for soft assignments of data points to clusters.
• Modeling Elliptical Clusters: The use of covariance matrices enables GMMs to model elliptical clusters, enhancing clustering performance.

Applications

• Anomaly Detection: GMMs are widely used in various applications, including anomaly detection.

Important Considerations

• Covariance Types: The choice of covariance types (full, tied, diagonal, spherical) can significantly impact the performance of GMMs.

Follow-up Questions

• How do GMMs compare to other clustering algorithms in terms of scalability and computational efficiency?
• What are the implications of choosing different covariance types in GMMs?