The concept of a cost function is central to Model Optimisation, particularly during the training phase of a model.
A cost function (also called a loss function or error function) is a mathematical function used in optimization and machine learning to measure the difference between predicted values and actual values. It quantifies the error or “cost” of a model’s predictions. The main goal of most learning algorithms is to minimize this cost function, thereby improving model accuracy.
Common examples include:
- Mean Squared Error (MSE) for regression tasks.
- Cross-Entropy Loss for classification tasks.
Relation to Loss Function
- The loss function measures the error for a single data point.
- The cost function typically aggregates these errors over the entire dataset, often by taking an average.
- See also: Loss versus Cost function.
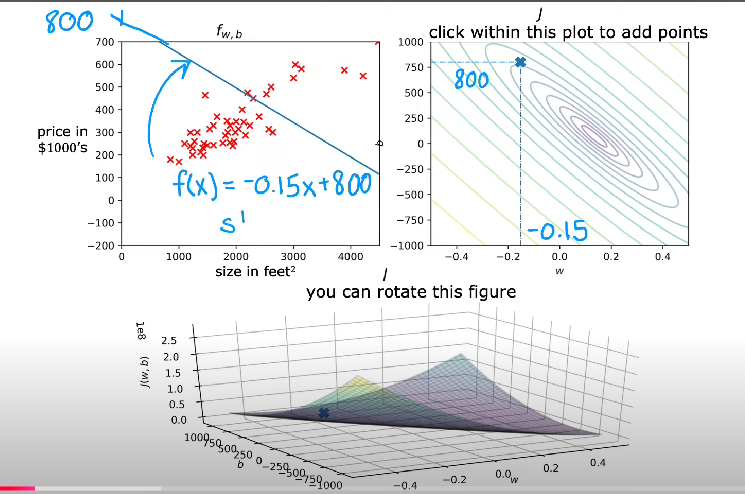
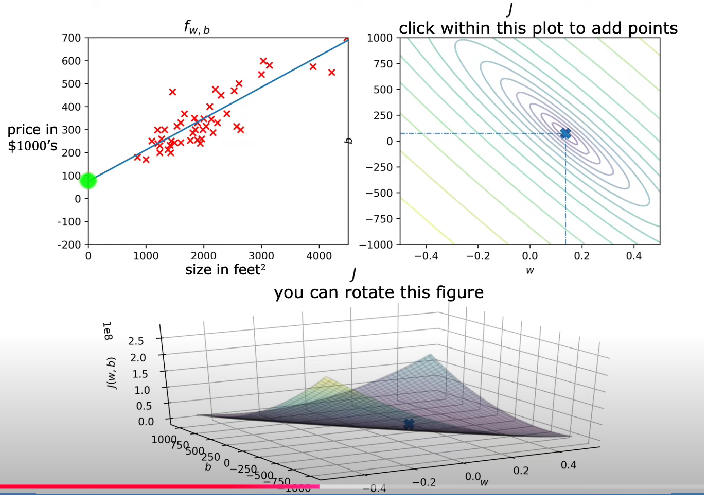
Parameter Space and Visualization
- Cost functions depend on Model Parameters.
- Plotting the cost function across the parameter space creates a surface that shows how different parameter values affect the cost.
- This surface often contains peaks and valleys, making optimization challenging.
Connection to Gradient Descent
- Gradient-based optimization methods use the cost function’s derivatives to iteratively update parameters toward the minimum.
Caveats
- The shape of the cost function depends on the dataset.
- There is often no explicit formula for complex models.
- Finding the global minimum can be challenging due to local minima and saddle points.
Summary
- A cost function is a specific type of objective function used to measure model error.
- It usually refers to empirical risk (average loss over all training samples).
Example (Linear Regression):
Images