Z-Normalisation

Z-normalisation, also known as z-score normalization, is a technique used to standardize the range of independent variables or features of data. This process is used in preparing data for machine learning algorithms, especially those that rely on distance calculations, such as k-nearest neighbors and gradient descent optimization.

Why Normalize?

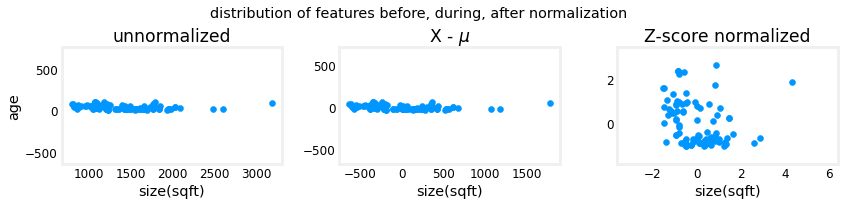
• Consistency Across Features: By normalizing, the peak-to-peak range of each column is reduced from a factor of thousands to a factor of 2-3. This ensures that each feature contributes equally to the distance calculations, preventing features with larger ranges from dominating the results.

• Centered Data: The range of the normalized data (x-axis) is centered around zero and roughly +/- 2. This centering is beneficial for algorithms that assume data is normally distributed around zero.

• Improved Learning Rates: Normalization allows for a larger learning rate in Gradient Descent, which can speed up convergence and improve the efficiency of the learning process.

Z-Score Normalization

Z-score normalization transforms the data so that each feature has:

• A mean of 0
• A standard deviation of 1

To implement z-score normalization, adjust your input values using the formula:

$x_j^{(i)}=\frac{x_j^{(i)}-{\mu }_j}{{\sigma }_j}$ Where:

• $x_j^{(i)}$ is the value of the feature $j$ for the $i$-th example.
• ${\mu }_j$ is the mean of all the values for feature $j$.
• ${\sigma }_j$ is the standard deviation of feature $j$.

The mean and standard deviation are calculated as follows:

${\mu }_j=\frac{1}{m}{\sum }_{i=0}^{m-1}{x}_j^{(i)}$

${\sigma }_j^2=\frac{1}{m}{\sum }_{i=0}^{m-1}(x_j^{(i)}-{\mu }_j{)}^2$

Where $m$ is the number of examples.

Examples

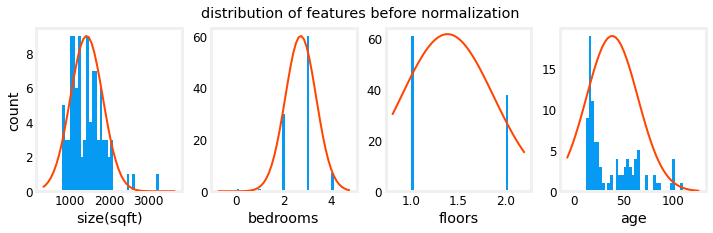
See that they are centred around 0.

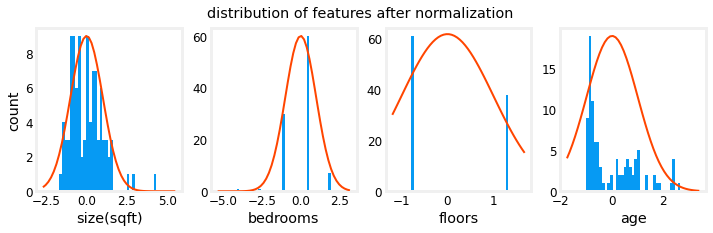
Below we see that its centered around 0 and been brought together.