Gradient Descent

Gradient Descent is an Optimisation function used to minimize errors in a model by iteratively adjusting its Model Parameters. It works by moving in the direction of the steepest decrease of the Loss function, reducing the Cost Function over time.

Core Idea

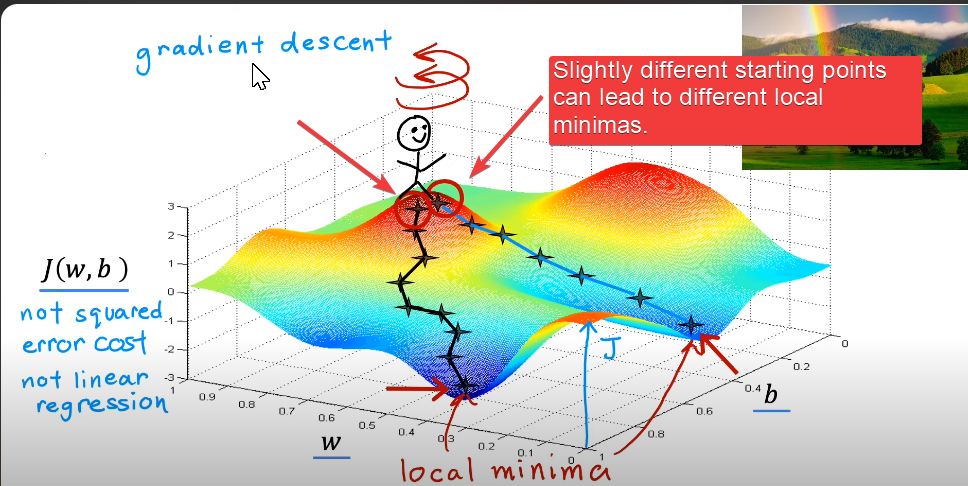
At any point on the cost function surface, gradient descent asks: “In what direction should I move to decrease the error most quickly?” The answer is the negative gradient.

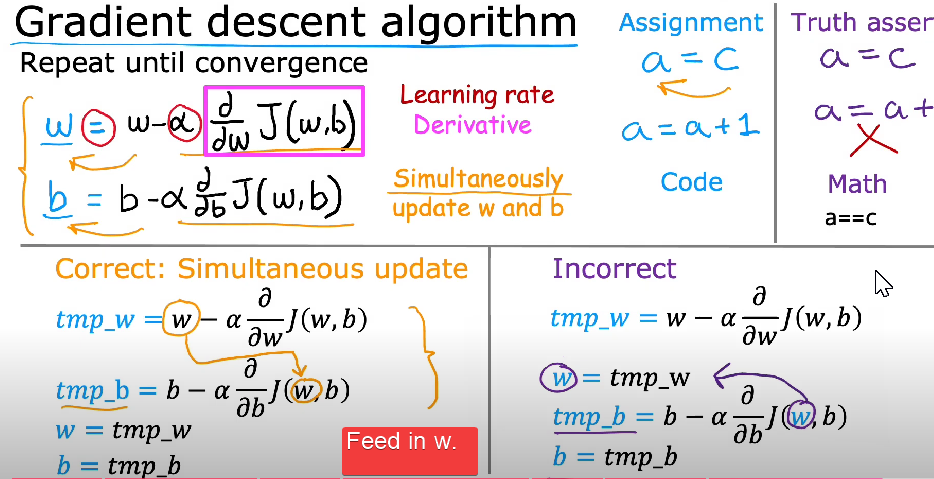
How It Works: Gradient Descent updates parameters using:

$$\theta =\theta -\alpha {\nabla }_{\theta }\text{Cost}(\theta )$$

Where:

• $\theta$ = model parameters.
• $\alpha$ = Learning Rate (controls step size).
• ${\nabla }_{\theta }\text{Cost}(\theta )$ = gradient of the Cost Function with respect to $\theta$.

Process

1. Compute the gradient of the Loss function with respect to parameters.
2. Update parameters in the opposite direction of the gradient.
3. Repeat until:
   • The cost converges (minimal change), or
   • Maximum iterations are reached.

Step Size Matters

• Too small: Convergence is very slow.
• Too large: May overshoot the minimum or diverge.

Variants of Gradient Descent

• Batch gradient descent: Uses the entire dataset for each update.
• Stochastic Gradient Descent: Updates after each single example (fast but noisy).
• Mini-batch gradient descent: Uses small subsets of data (balanced approach).

Key Insights

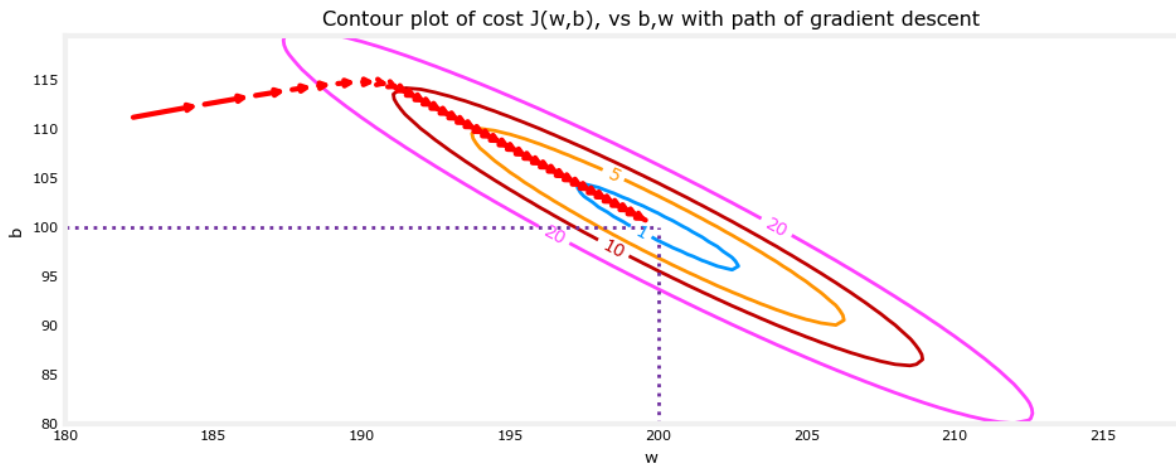
• Gradient Descent can be visualized using contour plots showing the path toward the minimum.

Notes

• Gradient descent uses the difference quotient for computing numerical derivatives.
• The Cost Function value vs. iterations should decrease over time.
• In online learning (e.g., Stochastic Gradient Descent), new data can be incorporated without recalculating the entire dataset.

Images