Naive Bayes

Can values for X,y be categroical ? Encoding Categorical Variables

BernoulliNB()

Why Naive Bayes?;;Order doesn’t matter, features are independent. Treated it as a Bag of words. Which simplifies the above equation.

Want to use this in classifiers for ML Want to understand: Multinomial Naive bayes classifer There is also: Gaussian Naive Bayes

Issues

To avoid having 0 probability sometimes they add counts $\alpha$ to do this.

Links:

https://youtu.be/PPeaRc-r1OI?t=169

Formula

$P(A|B)=P(A)\times \frac{P(B|A)}{P(B)}$ Think of the line as “given”.

Examples

Example 1

Example 2

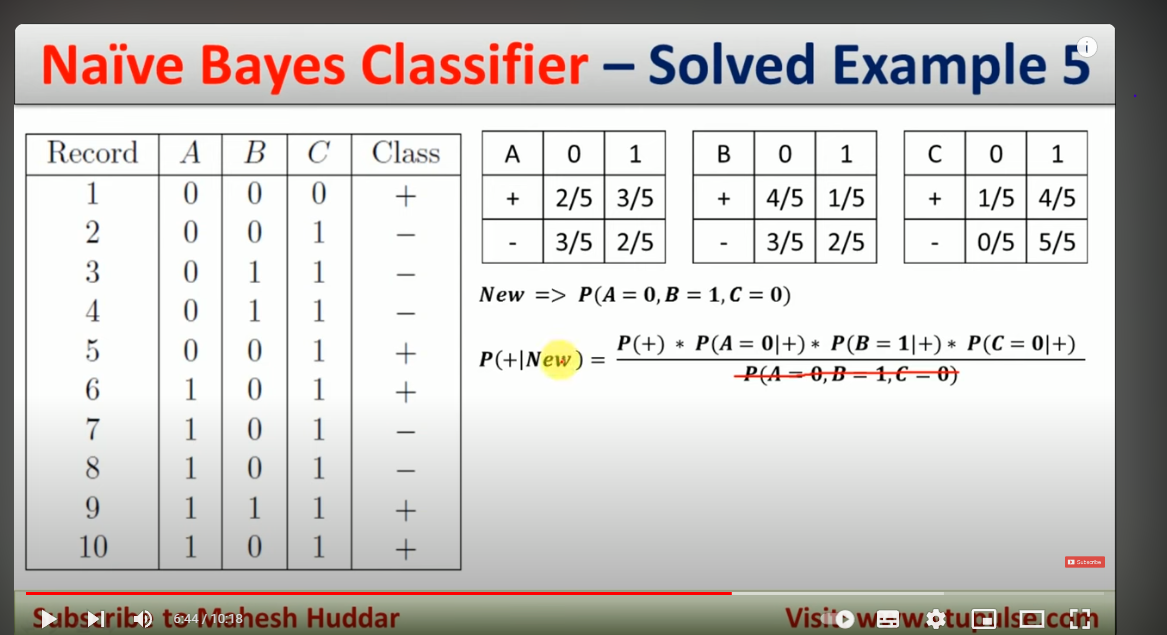
In the formula above P(A) is P(+), P(B)=P(NEW)

P(B|A) = P(A=0|+)*… *P(C=0|+)

P(A=0,B=1,C=0) is the same for both + and - class so remove.

Example Car accidents

What’s the probability of car having an accident given that driver is driving in summer, there is no rain, it’s a night and it’s an urban area?

Mock data:

Season	Weather	Daytime	Area	Did Accident Occur?
Summer	No-Raining	Night	Urban	No
Summer	No-Raining	Day	Urban	No
Summer	Raining	Night	Rural	No
Summer	Raining	Night	Urban	Yes
Summer	Raining	Day	Urban	No
Summer	Raining	Night	Rural	No
Winter	Raining	Night	Urban	Yes
Winter	Raining	Night	Urban	Yes
Winter	Raining	Night	Rural	Yes
Winter	No-Raining	Night	Rural	No
Winter	No-Raining	Night	Urban	No
Winter	No-Raining	Day	Urban	Yes
Spring	No-Raining	Night	Rural	Yes
Spring	No-Raining	Day	Rural	Yes
Spring	Raining	Night	Urban	No
Spring	Raining	Day	No	No
Spring	No-Raining	Night	Urban	No
Autumn	Raining	Night	Urban	Yes
Autumn	Raining	Day	Rural	Yes
Autumn	No-Raining	Night	Urban	No
Autumn	No-Raining	Day	Rural	No
Autumn	No-Raining	Day	Urban	No
Autumn	Raining	Day	Yes	No
Autumn	Raining	Night	Yes	No
Autumn	No-Raining	Night	No	No

To handle data like this it is possible to calculate frequencies for each case:

0. Accident probability

$P(Accident)=\frac{9}{25}=0.36$

$P(No-Accident)=\frac{16}{25}=0.64$

1. Season probability

Frequency table:

Season	Accident	No Accident
Spring	2/9	3/16	5/25
Summer	1/9	5/16	6/25
Autumn	2/9	6/16	8/25
Winter	4/9	2/16	6/25
	9/25	16/25

Probabilities based on table:

$P(Spring)=\frac{5}{25}=0.20$

$P(Summer)=\frac{6}{25}=0.24$

$P(Autumn)=\frac{8}{25}=0.32$

$P(Winter)=\frac{6}{25}=0.24$

$P(Spring|Accident)=\frac{2}{9}=0.22$

$P(Summer|Accident)=\frac{1}{9}=0.11$

$P(Autumn|Accident)=\frac{2}{9}=0.22$

$P(Winter|Accident)=\frac{4}{9}=0.44$

2. Weather probability

Frequency table:

	Accident	No Accident
Raining	6/9	7/16	13/25
No-Raining	3/9	9/16	12/25
	9/25	16/25

Probabilities based on table:

$P(Raining)=\frac{13}{25}=0.52$

$P(No-Raining)=\frac{12}{25}=0.48$

$P(Raining|Accident)=\frac{6}{9}=0.667$

$P(No-Raining|Accident)=\frac{12}{25}=0.333$

3. Daytime probability

Frequency table:

	Accident	No Accident
Day	3/9	6/16	9/25
Night	6/9	10/16	16/25
	9/25	16/25

Probabilities based on table:

$P(Day)=\frac{9}{25}=0.36$

$P(Night)=\frac{16}{25}=0.64$

$P(Day|Accident)=\frac{3}{9}=0.333$

$P(Night|Accident)=\frac{6}{9}=0.667$

4. Area probability

Frequency table:

	Accident	No Accident
Urban Area	5/9	8/16	13/25
Rural Area	4/9	8/16	12/25
	9/25	16/25

Probabilities based on table:

$P(Urban)=\frac{13}{25}=0.52$

$P(Rural)=\frac{12}{25}=0.48$

$P(Urban|Accident)=\frac{5}{9}=0.556$

$P(Rural|Accident)=\frac{4}{9}=0.444$

Assemble:

Calculating probablity of car accident occuring in summer, when there is no rain and during night, in urban area.

Where B equals to:

• Season: Summer
• Weather: No-Raining
• Daytime: Night
• Area: Urban

Where A equals to:

• Accident

Using Naive Bayes:

$P(A|B)=P(Accident|Season=Summer,Weather=No-Raining,Daytime=Night,Area=Urban)$

$P(A|B)=\frac{P(Summer|Accident)P(No-Raining|Accident)P(Night|Accident)P(Urban|Accident)P(Accident)}{P(Summer)P(No-Raining)P(Night)P(Urban)}$

$P(A|B)=\frac{\frac{1}{9}\frac{6}{9}\frac{6}{9}\frac{5}{9}\frac{9}{25}}{\frac{6}{25}\frac{12}{25}\frac{16}{25}\frac{13}{25}}=\frac{0.111\cdot 0.667\cdot 0.667\cdot 0.556\cdot 0.36}{0.24\cdot 0.48\cdot 0.64\cdot 0.52}=\frac{0.0099}{0.038}=0.26$

---

$P(A)=P(Accident)$

$P(B)=P(Summer)P(No-Raining)P(Night)P(Urban)$

$P(B|A)=P(Summer|Accident)P(No-Raining|Accident)P(Night|Accident)P(Urban|Accident)$

What is the Bayes theorem?;; The formula is P(A|B) = P(B|A) * P(A) / P(B).

What are the main advantages of Naive Bayes, and when is it commonly used?;; simplicity, quick implementation, and scalability, used in text classification.

**When using Naive Bayes with numerical variables, what condition is assumed on the data?;; Naive Bayes assumes that numerical variables follow a normal distribution.

How does Naive Bayes perform with categorical variables? makes no assumptions about the data distribution.

What is Naive Bayes, and why is it called “naive”?;; Algo which uses Bayes theorem, used for classification problems. It is “naive” because it assumes that predictor variables are independent, which may not be the case in reality. The algorithm calculates the probability of an item belonging to each possible class and chooses the class with the highest probability as the output.

Naive Bayes Naive Bayes classifiers are based on Bayes’ theorem and assume that the features are conditionally independent given the class label.

Naive Bayes

• A probabilistic classifier based on Bayes’ theorem.
• Simple and fast, especially effective for text classification.