K-means clustering is an Unsupervised Learning algorithm that partitions data into (k) clusters. Each data point is assigned to the cluster with the nearest centroid.
The algorithm partitions a dataset into k clusters by assigning data points to the closest cluster mean. The means are updated iteratively until convergence is achieved.
In ML_Tools see: K_Means.py
Key Features
- Unsupervised Learning: K-means organizes unlabeled data into meaningful groups without prior knowledge of the categories.
- Hyperparameter k: The number of clusters must be specified beforehand. The optimal number of clusters can be determined using WCSS and elbow method.
Algorithm Process:
- Randomly choose k initial centroids.
- Assign each data point to the nearest centroid.
- Recalculate the centroids based on the current cluster assignments.
- Repeat steps 2 and 3 until convergence (i.e., centroids no longer change significantly).
Visualization: Scatterplots can be used to visualize clusters and their centroids.
Adaptability: K-means can be updated with new data and allows for comparison of changes in centroids over time.
The initial centroids can effect the end results.
To correct this the algo is run multiple times with varying starting positions.
The centroids are updated after each iteration.
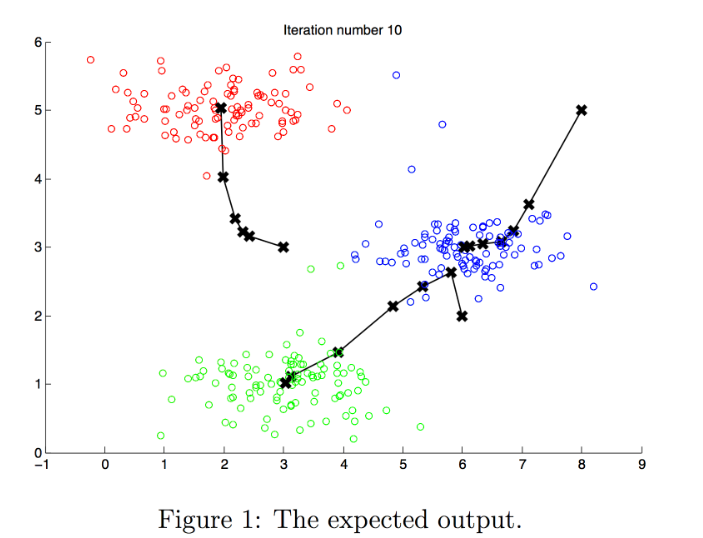
Limitations
- Sensitivity to Initialization: The algorithm is sensitive to the initial placement of centroids, which can affect the final clustering outcome.
- Predefined Number of Clusters: The number of clusters k must be specified in advance, which may not always be straightforward.