Model Parameters Tuning

To find optimal Model Parameters.

Finding Optimal Model Parameters

1. Parameter Space Exploration:

   • It’s useful to visualize slices of the parameter space by selecting two parameters at a time. This helps in understanding how different parameter values affect the model’s performance.

2. Cost Function

   • The cost function is used to find the minimum error in predictions. It measures the difference between predicted and actual values, and the goal is to minimize this function to improve model accuracy.

3. Optimisation function

   • Ideal parameters are found using optimization functions, which adjust the model parameters to minimize the loss function. Common optimization algorithms include Gradient Descent, Adam Optimizer, and Stochastic Gradient Descent.

4. Data Splitting:

   • Split the data into training and cross-validation sets to evaluate model performance. Plot the parameter of interest on the x-axis and accuracy on the y-axis to visualize performance.

Optimisation techniques

Example

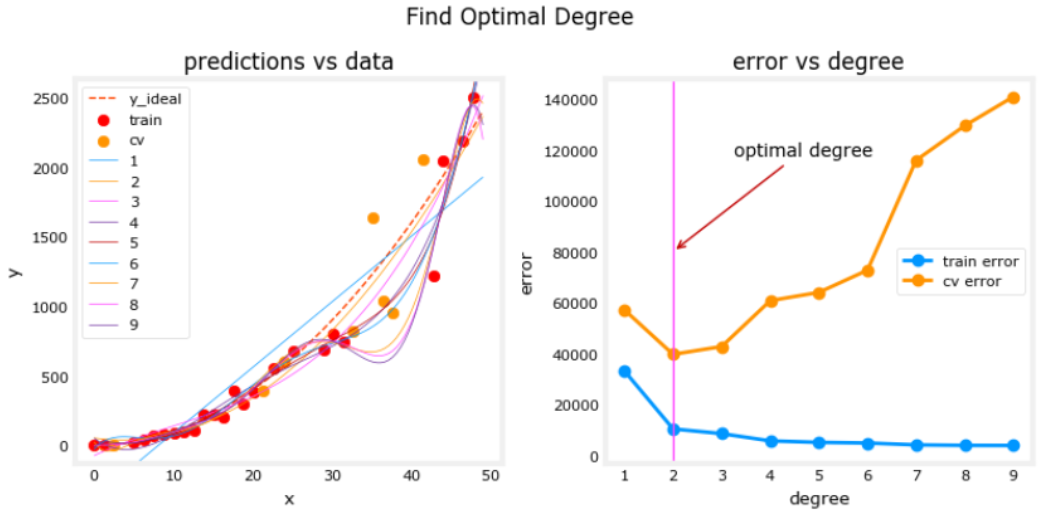
To find optimal model parameters, graph the parameter against error of the model.

On the left plot, the solid lines represent the predictions from these models. A polynomial model with degree 1 produces a straight line that intersects very few data points, while the maximum degree hews very closely to every data point.

On the right: - the error on the trained data (blue) decreases as the model complexity increases as expected - the error of the cross-validation data decreases initially as the model starts to conform to the data, but then increases as the model starts to over-fit on the training data (fails to generalize).