Non-negative Matrix Factorization

Non-negative Matrix Factorization (NMF) is a matrix decomposition technique that factors a non-negative matrix $V$ into two non-negative matrices $W$ and $H$ such that:

$$V\approx W\cdot H$$

In NLP, NMF is often applied to document-term matrices for topic modeling and feature extraction.

How NMF Works in NLP

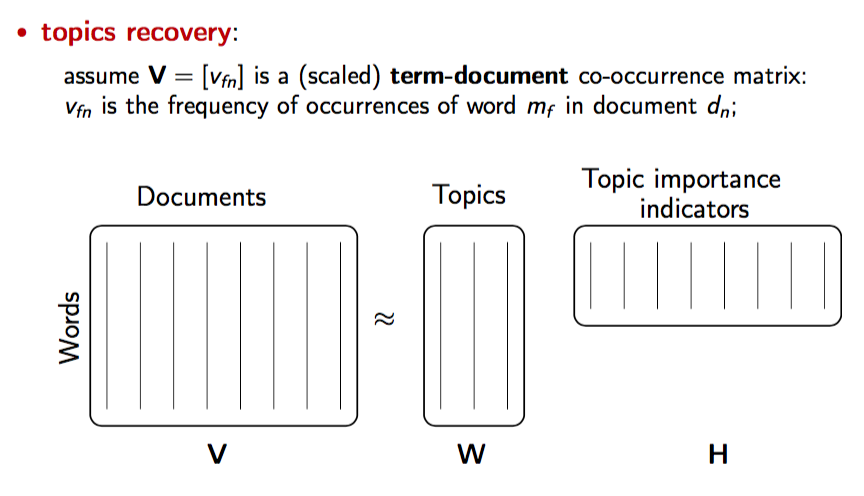
1. Construct a document-term matrix $V$:

   • Rows = documents
   • Columns = terms/words
   • Entries = term frequency (TF) or TF-IDF.

2. Decompose $V$ into:

   • $W$ (document-topic matrix): Each row represents the distribution of topics for a document.
   • $H$ (topic-term matrix): Each row represents the distribution of terms for a topic.

3. Interpret topics:

   • Each topic is represented by a set of high-weight words from $H$.
   • Each document is represented by a mixture of topics from $W$.

Application to Topic Importance Indicators

• Topic Importance for Documents: Look at $W$ to see which topics dominate a document.
• Key Words for Topics: Look at $H$ to find top terms per topic, which serve as indicators of the topic’s content or importance.
• Ranking Features: Terms with higher weights in $H$ are more important for defining a topic.

Benefits

• Produces interpretable topics because all entries are non-negative.
• Works well with sparse and high-dimensional NLP data.
• Can complement feature importance analysis in text classification and clustering.

Example (Python, using TF-IDF)

from sklearn.decomposition import NMF
from sklearn.feature_extraction.text import TfidfVectorizer
 
documents = ["I love NLP", "Machine learning is fun", "NLP and ML are related"]
vectorizer = TfidfVectorizer()
V = vectorizer.fit_transform(documents)
 
nmf = NMF(n_components=2, random_state=42)
W = nmf.fit_transform(V)  # document-topic matrix
H = nmf.components_       # topic-term matrix

• Rows of $H$ → important words per topic (topic indicators)
• Rows of $W$ → importance of topics per document

Image